Rechnen mit den Cuisenaire-Stäbchen

Eine praktische Handreichung für Lehrer an der Unterstufe
(leicht erweitert am 20. April 2005)

1. Mathematik-Unterricht im Wandel

Hierzulande konzentrierte sich der Mathematikunterricht in der Primarschule bis gegen 1970 weitgehend auf die Einübung in die Arithmetik (Rechnen mit Zahlen). Im Zentrum stand das nicht in Frage gestellte Zehnersystem, und der Rechenunterricht – wie er durchaus zu Recht hiess – setzte sich zum Ziel, dass die Schüler einerseits klare Zahlbegriffe hatten und die Grundoperationen „mündlich“ (d.h. beim Kopfrechnen) und schriftlich beherrschten und andererseits in der Lage waren, ihre arithmetischen Fertigkeiten in angewandten Aufgaben („Sätzchenrechnungen“) anzuwenden.

Dieser Rechenunterricht wurde nun einer fundamentalen Kritik unterzogen, was dazu führte, dass die Lehrpläne und Lehrmittel heute in praktisch allen Kantonen der Schweiz den neuen Strömungen angepasst wurden. Als Initialzündung für die Total-Kritik am überlieferten Rechenunterricht wird oft der sog. „Sputnik-Schock“ genannt, von dem die Amerikaner im Jahre 1957 heimgesucht wurden, als sie feststellen mussten, dass ihnen die Russen in wissenschaftlicher Hinsicht offenbar überlegen waren.

Die traditionelle Gestaltung des Rechenunterrichts mit seiner starken Betonung der Arithmetik wurde durch drei Hauptargumente in Frage gestellt:

• Als erstes warf man dem Rechenunterricht vor, er fixiere das Denken in ganz bestimmte Bahnen und verhindere das Aufkommen eines eigentlich mathematischen Denkens. Dieses sei flexibel, allgemein und kreativ und lasse sich nicht entwickeln durch die Fixierung auf das Zahlensystem und die Einübung in dessen Umgang mittels der Grundoperationen. Es gehe darum, das Kind den Umgang mit abstrakten Mengen und logischen Verknüpfungen zu lehren. So wurde die Mengenlehre – bisher ein Gebiet der höheren Mathematik, das an der Universität gelehrt wurde – zur Grundlage der gesamtem Mathematik (inklusive der Arithmetik) und des Mathematikunterrichts erklärt. Als Übungsmaterial wurden vom amerikanischen Professor Dienes die sog. „logischen Blöcke“ (Merkmalblöcke, Sabemat) entwickelt.

• Zweitens warf man dem bisherigen Rechenunterricht vor, er fixiere die Arithmetik auf das Zehnersystem; dieses sei aber bloss eine Möglichkeit unter vielen und – von mathematischem Standpunkt aus betrachtet – rein zufällig gewählt. Die Notwendigkeit der Infragestellung des Zehnersystems wurde belegt durch die Verwendung des Dualsystems (Zweiersystems) in der Computertechnik.

• Drittens wurden etwa gleichzeitig die ersten elektronischen Taschenrechner auf den Markt geworfen. Sie waren anfänglich noch teuer, wurden aber sehr rasch billiger. (Noch ca. 1970 zahlte man für einen Taschenrechner, der nicht viel mehr zustande brachte als die vier Grundoperationen, das Potenzieren und das Wurzelziehen, volle siebenhundert Franken.) Damit schien es, der moderne Mensch brauche auch gar nicht mehr rechnen zu können, da die Maschine dies alles schneller und zuverlässiger erledige. Aufgabe des Mathematikunterrichtes sei es, die Lösungswege zu erarbeiten, aber die rechnerische Arbeit könne man ruhig der Maschine überlassen.

Ich verzichte an dieser Stelle darauf, aus pädagogischer Sicht auf die Berechtigung der erwähnten Argumente einzugehen. Ich stelle lediglich fest, dass die Erneuerung des Mathematikunterrichts – wie nicht anders zu erwarten – zu einem sehr merklichen Leistungsabfall im arithmetischen Bereich geführt hat, und da ich nicht nur davon überzeugt bin, dass auch der heutige Mensch im Alltag den schnellen (nicht-maschinellen) Umgang mit Zahlen beherrschen sollte, sondern dass auch das Operieren mit Zahlen etwas mit Denken zu tun hat und darum das Rechnenkönnen durchaus auch als ein Gradmesser für Denkenkönnen gelten darf, bedaure ich diese Entwicklung. Ich möchte darum gerne jedem Primarlehrer empfehlen, die Bildung von arithmetischen Fertigkeiten als legitimes und notwendiges Ziel des Unterrichts anzuerkennen.

Was ich im folgenden darlege, ist herausgewachsen aus meiner eigenen Praxis, als ich nicht – wie in den letzten 25 Jahren meiner Lehrtätigkeit – Lehrer auszubilden hatte, sondern als Primarlehrer eine Dorfschule von der 1. bis 8. Klasse führte und in den höheren Klassen die Früchte eines wohl fundierten Rechenunterrichts auf der Unterstufe ernten konnte. Meine Ausführungen stimmen indessen mit jenen Erkenntnissen überein, die ich bei meinen lernpsychologischen, entwicklungspsychologischen und didaktischen Studien an der Universität gewonnen habe. Die vorliegende Arbeit erhebt nicht den Anspruch, den ganzen Mathematik-Unterricht abzudecken. Ich beschränke mich bewusst auf die Arithmetik. Ich will auch nicht behaupten, was ich vorschlage, sei der einzig mögliche Weg. Ich stelle lediglich fest, dass ich damit sehr gute Erfolge erzielte.

Ich habe schon sehr bald den Rechenunterricht auf der Unterstufe konsequent abgestützt auf die Methode Cuisenaire und dabei die Erfahrung gemacht, dass die Schüler gründlich und zuverlässig rechnen lernten. Ich betrachtete die Lehrplanziele stets als Minimalziele und hielt es darum für berechtigt, mit den Erst-, Zweit- und Drittklässlern in gewissen Gebieten deutlich über den Lehrplan hinauszugehen. So führte ich die Multiplikation bereits in der 1. statt in der 2. Klasse ein und übte die Division (unterschieden in Messen und Teilen) schon in der 2. Klasse. In der zweiten Klasse (teilweise schon in der ersten) legte ich die Grundbegriffe des Bruchrechnens (damals vorgesehen in der 6. Klasse). In der zweiten Klasse automatisierte ich nicht bloss das kleine Einmaleins, sondern sämtliche möglichen Multiplikationen, deren Produkte zwischen 1 und 100 liegen. Ich liess die Schüler auch die vorgesehenen Zahlräume (1. Klasse bis 20, 2. Klasse bis 100, 3. Klasse bis 1000) im Rahmen ihrer entwickelten Zahlbegriffe beliebig überschreiten. Schliesslich führte ich bereits in der 2. Klasse Klammerausdrücke ein, eine Massnahme, die vor 35 Jahren noch nicht im Lehrplan der Primarschule vorgesehen war.

2. Positive Beziehung zum Üben

Dies alles war freilich nur möglich, weil ich gerne mit den Schülern übte und das Üben nicht als „sturen Drill“ betrachtete, sondern als etwas, das zum Menschen gehört und durchaus der Natur des Kindes entspricht. Ganz allgemein kann man keine wirklichen Lernergebnisse erwarten, wenn man nicht alles, was man einbringt, gründlich übt. Üben heisst Wiederholen und in nahen Gebieten erneut anwenden. Wesentlich ist, die Schüler erfahren zu lassen, dass sie durch das Üben zu wirklichen Lernerfolgen kommen. Bei all dem ist entscheidend, dass die Kinder selber gerne üben, d.h. mit Freude und Eifer bei der Sache sind.

Die wichtigste Übung bestand darin, so oft wie möglich (möglichst täglich) die sinnlichen Veranschaulichungen der bereits erarbeiteten arithmetischen Erkenntnisse mittels des Cuisenaire-Materials zu wiederholen. Es hat keinen Sinn, dieses Anschauungsmaterial bloss punktuell zu verwenden, sondern die Schüler müssen damit so vertraut gemacht werden, dass sie die vorgesehenen Handlungen beinahe im Schlaf vollziehen können.

Ferner machte ich regelmässig im Anschluss an das reale Handeln mit den Farben-Stäbchen gezielte Übungen, um das mit den äusseren Sinnen Erfahrene in der inneren Vorstellung zu festigen.

Ein wesentlicher Teil des Übens dient dem Automatisieren von grundlegenden Rechenvorgängen. Keinesfalls darf dies auf ein unverstandenes Auswendiglernen von Rechnungen hinauslaufen. Dem Automatisieren müssen das reale Handeln, die sinnliche Anschauung und die klare Einsicht in die Zusammenhänge vorausgehen, und man muss auch dann, wenn eine Sache (z.B. das Einmaleins) automatisiert ist, immer wieder auf die Anschauung und die Einsicht zurückgreifen. Das Automatisieren darf auch nie zu früh vorgenommen werden, sondern darf erst einsetzen, wenn die reale Anschauung in der inneren Vorstellung repräsentiert ist.

Es gehört zum Wesen des Automatisierens, dass sich die richtigen Ergebnisse rasch einstellen. Es ist darum im Rahmen dieses Lernziels ebenso wenig anrüchig, die Uhr zur Messung der Leistungen zu gebrauchen, wie etwa im Sport oder im Instrumentalspiel (Fingerfertigkeit). Wichtig ist, dass die Schüler daran Freude haben, dass der Automatisation die gründliche Anschauung vorangeht, dass die Zeitmessung nicht den Denkprozess stört und nicht zu sozialen Abwertungen führt. Konkret: Ich schrieb z.B. alle möglichen Multiplikationen, deren Produkte zwischen 1 und 100 liegen, immer dann auf kleine Kärtchen, wenn wir die entsprechende Produktzahl gründlich betrachtet und besprochen hatten, und gab diese Kärtchen den Schülern in eine eigens dafür vorgesehene Blechschachtel. Sie konnten dann damit nicht nur als Hausaufgabe üben, sondern setzten sich auch in der Schule in einer freien Zeit (wenn irgend eine andere Arbeit fertig gemacht war) zu zweit oder zu dritt zusammen und übten miteinander. Es bedeutete stets ein Erfolgserlebnis, wenn eines feststellte, dass es seine beispielsweise 40 Rechnungen heute in kürzerer Zeit als vor ein paar Tagen zu bewältigen vermochte. Gelegentlich forderte ein Zweitklässler, der sich seiner Sache sicher war, auch einen Dritt-, Viert- oder Fünftklässler heraus, und ich weiss nicht, was an einem solch fröhlichen Wettkampf unmoralischer sein sollte als an einem Schach- oder Fussballspiel. Niemals habe ich erreichte Zeiten mit Noten in Beziehung gesetzt, sondern das Üben mit der Uhr wurde von den Schülern als fröhlicher Denksport empfunden.

3. Die Bildung des Zahlbegriffs

Jede arithmetische Tätigkeit ist sinnlos, wenn sie nicht auf gefestigten Zahlbegriffen beruht. Kinder, die in irgendeiner Klasse im Rechnen versagen, verfügen zumeist nicht über gefestigte Zahlbegriffe. Wenn sie z.B. 32 hören, „sehen“ sie innerlich die beiden Ziffern, statt eine Anzahl von Elementen, die sich z.B. als dreimal zehn plus zwei oder 4 mal acht oder das Doppelte von sechzehn oder die Hälfte von vierundsechzig strukturieren lässt. Sie bringen es darum – insbesondere, wenn sie zur Legasthenie neigen (Diskalkulie) – auch fertig, 32 mit 23 zu verwechseln, obwohl die beiden Zahlen vorerst einmal kaum etwas miteinander gemein haben.

Erst- und Zweitklässler zeigen es dem Lehrer sehr deutlich, wenn sie noch nicht über gefestigte Zahlbegriff verfügen: Sie zählen (z.B. die Finger, die Äpfel, womit gerechnet wird). Ein Kind, das zählt statt rechnet, müsste für einen problembewussten Lehrer ein Alarmzeichen sein. Man merke sich: Wer zählt, rechnet nicht.

Das bedeutet allerdings nicht, dass das Kind nicht zählen können muss. Das Zählen ist an sich etwas sehr Elementares und muss auch geübt werden; es ist eine notwendige und berechtigte Übung, dass Erstklässler alle möglichen Gegenstände im Zimmer zählen und dann – als Zusammenfassung ihres Tuns – in einem klaren Satz feststellen (als Beispiel): „Ich habe die Blumenvasen gezählt. In unserem Zimmer gibt es vier.“ Dieses Zählen hat aber zu Beginn etwas durchaus Mechanisches an sich, die Schüler nennen die einzelnen Zahlen rein als Folge der vorausgehenden, nicht aber als Ausdruck eines gefestigten Begriffs.

Wenn es um Festigung von Zahlbegriffen geht, so ist die einstweilige ausschliessliche Orientierung am Zehnersystem gerechtfertigt. Das Zehnersystem liegt dem Menschen körperlich nahe (zehn Finger, zehn Zehen) und ist aufs engste mit der Sprache verknüpft. Sobald wir in andern Systemen rechnen, schaffen wir neue sprachliche Probleme. Für das Kind – insbesondere für das schwächere – ist es auch nötig, dass es sich zuerst einmal an etwas Verbindlichem festhalten kann. (Nebenbei bemerkt: Auch wenn wir in andern Systemen rechnen, orientieren wir uns innerlich und sprachlich an den Zahlbegriffen, die auf das Zehnersystem bezogen sind.)

Fundamental für alles weitere ist somit die Bildung der Zahlbegriffe von 1 bis 10. Diese Begriffe sind dann gefestigt, wenn das Kind eine entsprechende Anzahl, die vor seinen Augen liegt, auf einen Schlag (ohne zu zählen) identifizieren kann, und zwar völlig fehlerfrei. Solange dies nicht geht, ist jede operative Verknüpfung von Zahlen (Addition, Subtraktion usf.) ohne Fundament.

Nun muss man aber wissen, dass der Mensch in der Regel nur 4 Elemente auf einen Schlag in jeder beliebigen Anordnung identifizieren kann und dass darum die Vorgabe von 5 oder mehr Elementen immer gesetzmässig strukturiert sein muss. Dabei ist wichtig, dass das Kind die jeweilige Zahl nicht nur in einer optischen Gestalt (z.B. die Fünf des Würfelbildes) erkennt, sondern in jeder möglichen Kombination.

Beispiele:

Analog zur oben beschriebenen Übung mit der Automatisation von Multiplikationen wäre es ratsam, – beginnend mit 0, 1, 2, 3 usf. – jedes mögliche Zahlbild auf ein Kärtchen zu malen (z.B. mit Punkten) und diese Kärtchen von den Schülern in einem Schächtelchen aufbewahren zu lassen. Kommt eine neue Zahl dazu, werden die neuen Kärtchen hinzugelegt. Damit ist Material vorhanden, anhand dessen die Schüler in der Schule und zu Hause täglich zwei bis drei Minuten üben können.

Genau besehen, liegt in dieser Einübung in die Zahlbegriffe bereits die Anschauung der grundlegendsten Operation: der Addition. Ohne zu formulieren „Fünf plus drei gleich acht“ sieht das Kind, dass es so ist. Die ersten Additionen sind dann eigentlich bloss das bewusste Aussprechen dessen, was im Begriff bereits enthalten ist.

Man kann in der 1. Klasse nicht lange genug bei der reinen Beschäftigung mit den Zahlbegriffen verweilen. Übt man so lange im Raum von 1 bis 10, bis wirklich alles fehlerfrei sitzt, so ergeben sich Additionen und Subtraktionen in diesem Zahlenraum nachher wie von selbst.

Um zu vermeiden, dass sich die Schüler statt Zahl-Bilder Ziffern vorstellen, sollte man die Ziffern immer erst einführen und schreiben lassen, wenn gewährleistet ist, dass sich im Kinde die Zahlvorstellung gefestigt hat. Im allgemeinen schreiben die Erstklässler viel zu früh Ziffern und „Rechnungen“. Je länger man bei der sinnlichen Anschauung verweilt und diese in gesprochener Sprache (nicht als geschriebene Ziffern) fasst, desto fester ist das Fundament für den ganzen späteren Rechenunterricht.

4. Das Cuisenaire-Material

Was bis jetzt dargelegt wurde, entspricht durchaus dem Rechenunterricht, wie wir ihn seit Pestalozzi kennen. Als Veranschaulichung der strukturierten Anzahlen kann alles nur Erdenkliche dienen: Blumen, Äpfel, Sterne, Scheibchen usf. Am Schluss sind es bloss noch Punkte.

Das neue Material, das der belgische Schulinspektor Cuisenaire in den fünfziger Jahren mit seinen Farbenstäbchen vorgelegt hat, ermöglicht die erneute Erfassung einer symbolisierten Zahl als unstrukturierte Einheit. Ganz bewusst wurde auf eine Zentimeter-Markierung verzichtet. Das Siebnerstäbchen ist einfach schwarz, und dass es gerade 7 cm lang ist und einen Querschnitt von 1 cm² hat, erfahren die Schüler erst viel später, wenn die Längen-, Flächen- und Raummasse eingeführt werden. Dass „darauf“ ein karminrotes und ein hellgrünes Stäbchen – d.h. ein Vierer- und ein Dreierstäbchen – Platz haben, entdeckt es in spielerischer Erfahrung und verfestigt sich in seiner inneren Vorstellung. Jedes Zahlenstäbchen wird verstanden als „eigene Persönlichkeit“, die in einer spezifischen Weise mit andern verwandt oder eben nicht verwandt ist.

Die Farben sind dementsprechend nicht zufällig gewählt. Zwei gelbe Stäbchen sind so lange wie ein oranges, zwei hellgrüne ergeben ein dunkelgrünes, ein dunkelgrünes und ein hellgrünes (bzw. drei hellgrüne) sind so lange wie ein blaues, zwei rote sind gleich lang wie ein karminrotes, und zwei karminrote (bzw. 4 rote, bzw. 2 rote und ein karminrotes) ergeben die Länge eines braunen. Die Einheit eins ist in allen enthalten, und darum ist das Einerstäbchen (Einerwürfelchen) weiss. In keiner der andern Zahlen ist die Sieben enthalten, und darum ist das entsprechende Stäbchen schwarz.

5. Erster Umgang mit dem Cuisenaire-Material

Es hat sich in meinem Unterricht bewährt, den oben beschriebenen konventionellen Aufbau von Zahlvorstellungen zeitlich zu kombinieren mit einem parallel verlaufenden, aber in sich eigenständigen Lehrgang anhand des Cuisenaire-Materials. Ich beschreibe im folgenden diesen Lehrgang, erinnere aber daran, dass in den ersten paar Wochen der 1. Klasse parallel dazu die Festigung des Zahlbegriffs im herkömmlichen Sinne geübt wurde. (Man wird sich fragen: Wo ist da das Mathematik-Lehrmittel. Ich muss sagen: Ich habe es weggelegt und erst wieder ab der 3. Klasse verwendet. Schriftliche Rechnungen haben die Schüler entweder selber erfunden (siehe später) oder habe ich selbst geschrieben und vervielfältigt, stets in Anlehnung an meinen eigenen Lehrgang.)

Grundsätzlich gilt: Wer mit dem Cuisenaire-Material arbeiten will, muss dies konsequent und gründlich tun. Ein bisschen nippen bringt gar nichts.

Als erstes liess ich die Erstklässler mit den „farbigen Stäbchen“ (später: „Zahlenstäbchen“) frei spielen. Sie bauten Türme, Häuser und was ihnen einfiel oder legten die Stäbchen auf den Tisch und „zeichneten“ mit ihnen allerlei.

Dann führte ich die Bezeichnungen der Farben ein. Durchaus nicht alle Erstklässler kennen die Farben. Das Viererstäbchen bezeichnete ich als „karminrot“, das Dreierstäbchen als „hellgrün“, das Sechser als „dunkelgrün“. Ich liess die Schüler Sätze bilden (Unterrichtssprache: Dialekt) und achtete – auch in der Mundart – auf deutliche Artikulation. Beispiele: „Ich lege ein dunkelgrünes Stäbchen zu einem karminroten. Sie sind zusammen so lang wie ein oranges.“ „Ich baue eine Brücke. Ich nehme zwei rote Stäbchen und lege darauf ein braunes.“

Dann folgte die Einführung der Begriffe „länger als“ und „kürzer als“. Beispielsätze: „Das orange Stäbchen ist länger als das blaue Stäbchen.“ „Das gelbe Stäbchen ist kürzer als das schwarze Stäbchen.“ Im Zuge dieser Übung liess ich die Schüler zwei beliebige Stäbchen in die auf dem Rücken gehaltenen Hände nehmen (z.B. nahm eines ein gelbes und ein braunes) und forderte eines dann etwa auf: „Zeige das gelbe vor.“ So mussten sie die Länge mit den Fingern abtasten. Überhaupt ist es ein Vorteil des Cuisenaire-Materials, dass es nicht nur die den Kindern angeborene Freude am Farbigen, sondern auch ihren Tastsinn anspricht.

All diesen Übungen, die auf Festigung von Begriffen (Zahlbegriffen und andern) abzielen, liegt das Bestreben zu Grunde, die Anschauung in Vorstellung zu verinnerlichen und das Erlebte sprachlich korrekt zu fassen.

Eine wichtige Übung ist das Herstellen der Treppe. Dazu wird als „Boden“ ein oranges Stäbchen gelegt, und alle 10 Stäbchen werden als Treppe (von links nach rechts und umgekehrt; beides üben) senkrecht dazu aufgereiht (stellen oder legen). Man fordert zuvor die Schüler auf, von jeder Farbe ein Stäbchen aus der Schachtel zu nehmen, von der orangen aber zwei. Ist die Treppe fertiggestellt, werden die Stäbchen wieder durchmischt, und das Ganze beginnt von vorne. Das kann man vier oder fünfmal wiederholen (jeden Tag über einige Zeit hinweg) und auch als kleines Wettspiel ankündigen („Auf ‚Los‘ beginnt’s. Wer ist zuerst fertig?“)

Als nächstes sprechen wir mit den Schülern über die Farbfamilien: in der ersten Stunde nur über die gelbe (neben andern der obgenannten Übungen), in der zweiten über die blaue, in der dritten über die rote. Im Rahmen dieser Übung führen wir zwei sehr wichtige Begriffe ein: „das Doppelte“ („doppelt so lang“) und „die Hälfte“ (halb so lang). Hier lernen die Erstklässler wichtige Sätze sprechen: „Das orange Stäbchen ist doppelt so lang wie das gelbe.“ „Das gelbe Stäbchen ist halb so lang wie das orange,“ usf. Geht dies gut, so kann man beim Vergleich des blauen mit dem hellgrünen Stäbchen sogar die Begriffe „das Dreifache“ („dreimal so lang“) und „ein Drittel“ („dreimal kürzer“) einführen.

Können die Schüler alle Farbfamilien bilden und immer auch sagen, warum diese Stäbchen zusammengehören, so soll dies wiederum zu einer gewissen Fertigkeit geübt werden: Ausgehend von der Treppe werden die Farbfamilien gebildet: die gelbe, die blaue und die rote. Das weisse und das schwarze Stäbchen werden allein hingelegt. „Wer ist zuerst fertig? Und gerade nochmals. Und nochmals.“

Eine weitere Übung besteht darin, mit geschlossenen Augen durch Abtasten der Länge das richtige Stäbchen zu finden. Hier kann man nicht (wie bei den Zahlbegriffen) auf hundertprozentige Treffsicherheit hoffen, sondern man wird zufrieden sein, wenn es die Kinder immer besser können. Einzelne sind sehr bald so weit, dass sie jedes Stäbchen blind greifen und richtig der Farbe nach benennen können. Im Anschluss daran drängt sich folgende Übung auf: Die Schüler zeigen auf irgendwelche Gegenstände oder Teile davon und sagen, indem sie schätzen: „Dieser Stift ist so lang wie ein blaues Stäbchen,“ usf. Nach der Schätzung sollen sie es selbst nachprüfen. Man wird sehen, dass die Schüler sehr bald eine grosse Sicherheit an den Tag legen. Später, wenn die Längenmasse eingeführt sind und die Schüler erfahren haben, dass das Neunerstäbchen eben gerade 9 cm lang ist, machen sie sich einen Spass daraus, alle möglichen kurzen Strecken zu schätzen, und man wird feststellen, dass sie die Dinge oft zentimetergenau treffen. (Es geht eben auch beim Rechnen mit Massbezeichnungen nicht einfach darum, diese Abkürzungen – z.B. cm – als leere mathematische Grössen mitzuschleppen und mechanisch hinzuschreiben, sondern die Schüler müssen auch hier klare Vorstellungen und Begriffe haben.)

Fassen wir zusammen, was die Schüler bis jetzt können: Sie können die Stäbchen zählen, sie können sie beim Farbnamen nennen, sie können sie zur Treppe und in Farbfamilien anordnen, sie kennen die Begriffe „länger als“, „kürzer als“, „halb so lang“ („die Hälfte“) und „doppelt so lang“ („das Doppelte“), sie können sie blind greifen und dementsprechend meist richtig der Farbe nach benennen. Parallel dazu wurden Zahlbegriffe anhand anderer Materialien geübt: zuerst „ein“ – „viel“, dann die übrigen Zahlen.

6. Die Cuisenaire-Methode: Zahlbetrachtung anhand des Cuisenaire-Materials

Bis jetzt wurden bloss Grundbegriffe gebildet, aber es wurde nicht – im herkömmlichen Sinne – gerechnet. Die Stäbchen selbst wurden noch nicht mit Zahlen identifiziert. Die beschriebenen Übungen dürften etwa die Rechenstunden der ersten 5 bis 6 Wochen der 1. Klasse in Anspruch nehmen.

Nun ist darauf hinzuweisen, dass es nicht bloss Cuisenaire-Material gibt, sondern auch eine Cuisenaire-Methode. Sie beruht auf dem Prinzip, beim Rechnen nicht synthetisch, sondern analytisch vorzugehen. Mit andern Worten: Bei der herkömmlichen Methode geht man von der konkreten mathematischen Aufgabenstellung aus und sucht dann das Ergebnis. So fragt man: „Wieviel ergibt 4 plus 3?“ Oder: „Was ist 6 mal 7?“ Bei der Cuisenaire-Methode hingegen geht man vom „Ergebnis“ aus und fragt entsprechend: „Was alles ergibt 7?“ „Was alles ergibt 42?“ Der Unterschied ist klar: Bei der synthetischen Vorgehensweise wird dem Schüler ein Problem vorgesetzt, das praktisch nur eine Lösung zulässt, bei der analytischen wird er vor eine Problemsituation gestellt, die völlig offen ist und seiner Freiheit und Kreativität kaum mehr Grenzen setzt.

Der Unterschied, ob ich bei der Bildung der arithmetischen Fertigkeiten synthetisch oder analytisch vorgehe, ist somit fundamental. Für mich ist daher die Anwendung der analytischen Methode nicht einfach eine Frage des Geschmacks, sondern sie steht in Übereinstimmung mit dem pädagogischen Grundsatz, die Eigentätigkeit des Kindes in Anspruch zu nehmen und zu fördern und seine Kreativität auszubilden.

Ich habe erfahren, dass die Öffnung des Denkprozesses durch die analytische Methode im Kinde grosse Kräfte freisetzt und insbesondere seine Motivation zum Lernen steigert. Darüber hinaus entspricht die analytische Methode insofern der Idee der Gerechtigkeit, als ungleich begabte Schüler ihren jeweiligen Fähigkeiten gemäss gefordert werden können, ohne versagen zu müssen.

Die grundlegende Tätigkeit beim analytischen Vorgehen ist die Zahlbetrachtung. Was darunter zu verstehen ist, möchte ich anhand einer Arbeitseinheit aus der 2. Klasse zeigen. Im Prinzip geht es aber in der 1. Klasse um dasselbe.

Geht man synthetisch von den Aufgabenstellungen (z.B. Addition und Subtraktion im Raume 0 bis 40) aus, so erlebt der Schüler eigentlich alle Zahlen als gleichwertig – eine reiht sich an die andere, und 23 ist beispielsweise nichts wesentlich anderes als 24 (z.B. 16 + 8 = 24 / 11 + 7 = 18 / 31 – 9 = 22 / 28 – 5 = 23). Nun sind aber die Zahlen – z.B. zwischen 1 und 100 – nicht gleichwertige Elemente einer unstrukturierten Aufreihung, sondern jede Zahl hat ihren eigenen Charakter, und es gibt solche, die wichtiger sind als andere und eine ganz besondere Ausstrahlung haben. Durch die analytische Zahlbetrachtung tragen wir diesem Umstand Rechnung, und jede Zahl wird erfahren als eine Persönlichkeit mit einem eigenen Charakter und mit unverwechselbaren Bezügen.

Die Auswahl jener Zahlen, die wir ins Zentrum unserer Betrachtung stellen, ist darum nicht zufällig. In der zweiten Klasse begann ich jeweils mit der Zahl 25 und schritt über die 50 zur 100. Das war leicht und eigentlich mehr oder weniger eine Vertiefung dessen, was sie in der 1. Klasse bei der Erweiterung des Zahlrenraums bis 100 gelernt hatten. Dann wählte ich die Zahl 24. An diesem Beispiel möchte ich zeigen, was Zahlbetrachtung konkret bedeutet.

In der 24 „kreuzen“ oder „begegnen“ sich (neben der 1 und der 24) die 2, die 3, die 4, die 6, die 8 und die 12. (Die 23 hingegen bekommt – ausser der 1 und sich selbst – „keinen Besuch“.) Bei der Betrachtung der 24 können die Schüler – ganz ihren Begabungen und ihrem Interesse entsprechend – diese Bezüge selber entdecken, und sie können grundsätzlich unendlich viele Aufgaben erfinden, die schliesslich 24 ergeben. So liess ich die Schüler zuerst zwei orange und ein karminrotes Stäbchen hinlegen, und dann konnten sie allerlei „Züge“ oder „Linien“ (d. h. Aufreihungen von weiteren Stäbchen) bilden, die gleich lang waren. Fragte ich sie dann, was alles 24 ergebe, so hörte ich etwa:

10 + 6 + 8 = 24

1 + 2 + 3 + 4 + 5 + 6 + 3 = 24

2 + 5 + 7 + 1 + 4 + 5 = 24

oder 8 + 8 + 8 = 24, was dann kürzer gesprochen wurde: dreimal 8 = 24

aber auch 7 + 7 + 7 + 3 = 24, was als „dreimal 7 + 3“ abgekürzt und später als (3 x 7) + 3 geschrieben wurde. Anmerkung

Die „Züge“ mit lauter gleichfarbigen „Wagen“ griffen wir heraus und bildeten daraus ein „Bödeli“ Hochdeutsch: Zahlfeld): 3 x 8 / 4 x 6 / 6 x 4 / 8 x 3 / 12 x 2 (auch: 2 x 12).

Je zwei Zahlfelder liessen sich als deckungsgleich aufeinander legen, so dass offensichtlich wurde, dass 4 x 6 gleich viel gibt wie 6 x 4, aber nicht dasselbe ist.

Das Zahlfeld 6 x 4 liess sich auch leicht in 3 x 8 umwandeln, indem man von den 6 Viererstäbchen die Hälfte nahm und sie der andern Hälfte „anhängte“. Dann wurde auch ein Gesetz deutlich, das ich hinfort bei allem Rechnen immer anwandte: Multiplikationen lassen sich verwandeln (vereinfachen) indem man den einen Faktor halbiert, den andern verdoppelt (bzw. drittelt und verdreifacht usf.). Später war es kein Problem, z. B. 36 x 42 zu rechnen, denn das ist 21 x 72 und auch 7 x 216.

Natürlich erkundigten wir uns auch nach „dem Doppelten“ und dem „Vierfachen“ von 24 und sahen dann den Zusammenhang mit 48 und 96: Wenn 3 x 8 = 24 ist, so ist eben 6 x 8 = 48 und 12 x 8 = 96. Aber das war erst ein Ausflug in das Thema der nächsten Woche, wo dann nicht (als Fortsetzung von 24) 25 an die Reihe kam, sondern eben 48 und später 96. Diese Zahlen warfen bei ihrer Betrachtung wieder ein Licht zurück auf die 24, und was dort gelernt wurde, konnte jetzt in neuem Zusammenhang angewandt werden. Es leuchtete ein, dass wenn 6 x 8 = 48 ist, die Rechnung 6 x 16 = 96 genau so einfach ist.

Das Teilen liess sich ganz einfach zeigen: Ich nahm ein karminrotes Zahlfeld (6 x 4) und liess es sanft auf die Tischfläche fallen. Die 24 wurde in 6 gleiche Teile geteilt: 24 : 6 = 4. Das Teilen ging Hand in Hand mit dem Multiplizieren. Auch das Messen wurde hier schon vorbereitet: Ich fragte z.B., wie viele braune Stäbchen auf der „24-er-Linie“ Platz haben. In der 3. Klasse wurde dann so gesprochen: 24 gemessen mit 8 geht 3 mal.

Hatte ich intensiv mündlich, anhand des Materials mit den Schülern geübt, so erfolgte das schriftliche Üben im Heft. Wer wollte, konnte einfach die in Form von farbigen Stäbchen hingelegten „Linien“ und „Bödeli“ abschreiben. Wer wollte, konnte eigene Rechnungen machen, die 24 ergaben. Dies war die einzige Bedingung. Und da erlebte ich oft, dass sich z.B. schwächere Schüler ganz vorsichtig vom Anschauungsmaterial lösten, indem sie sich Schritt für Schritt vorantasteten:

Begabtere Rechner waren mutiger und erfanden kreuz und quer Rechnungen im Rahmen aller 4 Operationen und – als diese eingeführt worden waren – mit Hilfe von Klammern. Später (bei der Betrachtung anderer Zahlen) begannen ganz Pfiffige z.B. bei 1000 (die Erweiterung des Zahlenraums bereitete ihnen offensichtlich keine besondere Mühe) und machten eine Subtraktionsrechnung, die unten an der Heftseite z.B. mit 36 (oder was dann eben gerade im Zentrum stand) endete, und noch andere – von diesem Wahnwitz angesteckt – gingen auf ihrem Weg von 1000 hinunter zu (beispielsweise) 36 abwechselnd ab- und aufwärts, nur, um auf diese Weise mit einer einzigen Rechnung eine ganze Seite füllen zu können. Für die simplen „Biegeli-Rechnungen“ im gedruckten Rechnungsbüchlein hatten sie nur ein müdes Lächeln übrig.

Natürlich kam es vor, dass sie sich einmal bei ihrer Wanderung von 1000 (oder wo sie beginnen mochten) hinunter zum anvisierten Ziel verrechneten, aber darauf kam es nicht an, sondern nur darauf, dass sie rechneten. Die weiteren Denkprozesse mochten nach einem unbemerkten Fehler sehr wohl wieder richtig sein. Für mich als korrigierender Lehrer war darum nicht in erster Linie das richtige Resultat von Bedeutung, sondern der Umstand, dass die Schüler einen Denkvorgang richtig erfasst hatten und gewissenhaft übten. Es war mir auch gar nicht möglich, alle Rechnungen, die die Schüler erfanden, nachzurechnen. So machte ich Stichproben und drückte einen speziell angefertigten Stempel unten an die Seite:

All dies zeigt, dass die analytische Zahlbetrachtung der Freiheit und der individuellen Begabung des Schülers keine Grenzen setzt, während das synthetische Verfahren konkreter Problemvorgaben das Denken einschränkt und – da es sich ja um gleiche Kost für alle handelt – den unterschiedlichen Leistungsmöglichkeiten der Schüler keinerlei Rechnung trägt.

7. Zahlbetrachtung in der 1. Klasse

In der 1. Klasse ging es nun also darum, vorerst einmal die Zahlen zwischen 1 und 10 zu betrachten. Dabei begann ich ganz bewusst bei der 10, weil diese Zahl unser Zahlensystem trägt. Ich liess also hier jede mögliche Kombination zweier Stäbchen, die zusammen so lange sind wie ein oranges, hinlegen und forderte dann die Schüler auf, das orange Stäbchen mit lauter gleichfarbigen zu „füllen“. Möglich war 2 x 5, 5 x 2 und 10 x 1. Erst hier – und dann konsequent immer – nannte ich das orange Stäbchen erstmals „Zehnerstäbchen“, weil zehn „Einerli“ darauf Platz finden. Den meisten Kindern war der Rest ziemlich klar: Die farbigen Stäbchen bekommen neue Namen, je nach der Anzahl „Einerli“, die darauf Platz finden.

Einstweilen wurden noch Farbbezeichnungen und Zahlbezeichnungen der Stäbchen kombiniert (alles immer schön Schritt für Schritt, wie dies Pestalozzi mit seinem Prinzip der Lückenlosigkeit fordert): „Ein dunkelgrünes und ein karminrotes Stäbchen ergeben zusammen ein Zehnerstäbchen.“ Und dann kam das Spiel, das hinfort zu den Standardspielen gehörte: Ich hielt z.B. ein hellgrünes Stäbchen auf, und die Kinder mussten dann als Ergänzung zum Zehnerstäbchen das schwarze ergreifen und aufhalten. So konnte ich immer gleich sehen, wer richtig „gerechnet“ hatte. (Überhaupt kann man sich beim Üben des Kopfrechnens das Resultat mit den Cuisenaire-Stäbchen auf eine Aufforderung hin von allen Schülern gleichzeitig anzeigen lassen und hat sofort die Kontrolle.) Bei falsch angezeigten Resultaten gab ich mich nie damit zufrieden, dass das Kind, nachdem es den Fehler bemerkte, nun das richtige Stäbchen zeigte, sondern ich liess es die richtige Kombination mit den erforderlichen Stäbchen vor sich auf den Tisch legen. (Ich stelle immer wieder fest, dass z.B. Lehrerstudenten einfach auf richtige Resultate aus sind und ein Rechenproblem mit dem Kinde nicht mehr weiterverfolgen, sobald dieses das richtige Resultat genannt hat. Eine falsche Rechnung ist aber immer die Anzeige für einen unkorrekten Gedankengang, und darum besteht die richtige Reaktion des Lehrers auf eine falsche Antwort darin, dass er mit dem Schüler den Gedankengang – möglichst anhand einer klaren Anschauung – Schritt für Schritt durchgeht.)

Ich verweilte ziemlich lange bei der 10, so lange, bis alle möglichen Zweier-Kombinationen, die 10 ergeben, gesichert waren. Ich führte nun die Benennung der übrigen Stäbchen mit ihrem Zahlennamen (Zweier-Stäbchen etc.) ein und verwendete hinfort diese Bezeichnungen. Ich achtete aber darauf, immer noch am Material zu bleiben und alle „Rechnungen“ handelnd mit den farbigen Holzstäbchen ausführen zu lassen. Je länger man am sichtbaren Material bleibt, desto grösser ist der Erfolg.

Sobald die 10 richtig „sass“, ging ich zur 9. Waren die Schüler sicher bei der Paarung von Stäbchen, die 9 ergeben, so vermischte ich Aufgaben, die 9, mit solchen, die 10 ergaben. Das Prinzip dürfte klar sein: Festigen des Bisherigen, dann ein neuer Schritt (jetzt z.B. die 8), dann Vermischung mit dem Bisherigen und erneute Festigung usf. Wer im Mathematik-Unterricht (und wohl nicht nur hier) Erfolg haben will, muss systematisch vorgehen.

8. Der Zehner-Übergang

Viele – insbesondere schwächere – Schüler scheitern im Rechnen erstmals, wenn es „über den Zehner“ geht. Im traditionellen Arithmetik-Unterricht nimmt man diese Klippe, indem man bewusst einen Einschnitt macht. So wird z.B. 8 + 5 zuerst verwandelt in 8 + 2 + 3, damit das Ergebnis 13 einleuchtet. Bei der Cuisenaire-Methode macht man diesen Einschnitt nicht, sondern man automatisiert – nachdem man von 10 her gegen 5 hin (der Rest ist dann klar) geschritten ist – alle Additionen bis hinauf auf 20. Betrachtet man z.B. die 11 (als Grundlage die Linie orange plus weiss), so werden eben alle Paarungen hingelegt, die 11 ergeben, und in gleicher Weise eingeübt, wie dies zuvor mit den Zahlen im ersten Zehner gemacht wurde.

Im allgemeinen wird in unserem Rechenunterricht nur das kleine Einmaleins automatisiert. Es hat sich mir gezeigt, dass es sich für alles weitere bis in die oberen Klassen lohnt, in der 1. Klasse auch alle Zweier-Paarungen, die als Summe irgend eine Zahl von 1 bis 20 ergeben, zu automatisieren. Das Kopfrechnen ist dadurch wesentlich einfacher. Man kann auch hier alle möglichen Paarungen auf Kärtchen schreiben und die Schüler damit üben lassen.

9. Der Zahlenraum bis 100

Wenn ich in der 1. Klasse die oben beschriebenen Übungen gemacht hatte, war eigentlich die Erweiterung des Zahlenraums in der Vorstellung und in der sprachlichen Bewältigung bis hundert eine leichte Angelegenheit. Zuerst rechneten die Schüler mit reinen Zehnern und legten entsprechend ungleich grosse orange Zahlfelder. Danach ging es darum, dass sie – vorerst ohne zu rechnen – die mit den Stäbchen veranschaulichten gemischten (Einer und Zehner) Zahlen erkennen und benennen und aufgrund des Gehörten richtig legen konnten. Solange dies nicht mit vollkommener Sicherheit geht, ist weitergehendes Rechnen sinnlos. Dann wurden erste Erweiterungen folgender Art versucht:

7 + 8 (schwarz + braun) = 15

orange + schwarz + braun = 25

17 + 8 = 25 usf.

Hier drang ich nicht mehr sehr in die Tiefe, sondern ich wollte lediglich den Zahlenraum bis 100 erweitern und die möglichen Analogien bewusst machen; alles weitere verlegte ich in die 2. Klasse.

10. Das Einmaleins

Im traditionellen Rechenunterricht lernen die Schüler „Reihen auswendig“. In der Cuisenaire-Methode wird darauf verzichtet, weil man eben nicht vom Problem (z.B. 1 x 6 / 2 x 6 / 3 x 6 usf.) ausgeht, sondern vom „Ergebnis“. Betrachte ich z.B. die 48, so begegnen sich hier Zweier-, Dreier-, Vierer-, Sechser-, Achter-, Zwölfer-, Sechzehner- und Vierundzwanzigerreihe. Und indem ich beim Üben jedes Zahlfeld einerseits halbiere, andererseits verdopple, so kommen alle Multiplikationen, die 24 oder 96 ergeben, in ihrem organischen Zusammenhang mit der 48 und allen entsprechenden Multiplikationen in den Blick.

Wie man sieht, wird auch nicht zwischen Multiplikationen aus dem kleinen Einmaleins und solchen mit zweistelligen Zahlen unterschieden: 4 x 12 wird genau so selbstverständlich eingesehen und geübt wie 8 x 6.

Es geht also darum, im Verlaufe der 2. Klasse (heute wird man vielleicht auch noch einen Teil der 3. einbeziehen) sämtliche Produktzahlen zwischen 1 und 100 – einzeln oder im Zusammenhang mit einer andern – zum Gegenstand der Betrachtung zu machen, so dass am Schluss alle möglichen Multiplikationen, deren Produkte zwischen 1 und 100 liegen, automatisiert sind. Ich habe nicht jedes Jahr dieselbe Reihenfolge gewählt, aber eine mögliche Abfolge sähe etwa so aus (es kommen nur Zahlen über 20 vor, weil alles, was darunter liegt, schon in der 1. Klasse gefestigt wurde):

25 50 100 75 | 20 40 80 | 24 48 96 | 36 72 | 21 42 84 63 | 28 56 | 32 64 | 27 54 81 | 30 60 90 | 35 70 | 45 90 | 49 98 | 22 44 88 | 33 66 99 | 55 77 | 26 52 | 39 78 | 65 | 91 | 34 68 | 38 76 57 | 46 92 69 | 51 85 | 29 58 87 | 62 | 93 | 74 | 82 | 86 | 94 | 95

Selbstverständlich hält man sich nicht bei jeder Zahl gleich lange auf. Die 84 beispielsweise gibt viel mehr her als etwa die 82. In obiger Aufreihung ist eine gewisse Systematik erkennbar. Es sind eigentlich Zahlengruppen, die nacheinander behandelt werden. Am Schluss haben die Schüler jede mögliche Multiplikation, deren Produkt nicht über 100 liegt, auf einem Kärtchen in ihrer Schachtel. Und da sie damit praktisch täglich üben, haben sie’s jetzt auch noch im Kopf.

11. Symbolisierung der 4 Grundoperationen

Bisher ist wohl klar geworden, dass die Addition ganz simpel veranschaulicht wird, indem man die Summanden (Stäbchen) auf eine Linie aneinander reiht. Um die Summe festzustellen, werden der Linie so viele Zehnerstäbchen wie möglich unterlegt, und der überragende Rest wird mit einem entsprechenden Stäbchen aufgefüllt.

Bei der Subtraktion wird zuerst der Minuend als Linie und darüber der Subtrahend hingelegt, wodurch die Differenz sichtbar wird (und allenfalls mit weiteren Stäbchen ausgemessen werden kann).

Multiplikationen werden als Zahlfelder symbolisiert, wobei man z.B. bei 3 x 7 quer über die drei schwarzen Stäbchen ein hellgrünes legt. Will man auf dem Tisch viele Multiplikationen symbolisieren, so geht das Material rasch zu Neige. Es leuchtet daher den Schülern durchaus ein, dass man – um im obigen Beispiel zu bleiben – von den drei schwarzen Stäbchen lediglich noch eins liegen lässt, so dass ein „Kreuz“ (unten schwarz, oben hellgrün) liegen bleibt. Sämtliche Multiplikationen lassen sich somit mit 2 Stäbchen (bzw. Linien) symbolisieren, wobei darauf zu achten ist, dass immer der erste Faktor oben liegt. Der angemessene Umgang mit den Zahlenstäbchen zeigt nämlich, dass das, was ein routinierter Mathematiker einander gleich setzt, durchaus nicht das Gleiche ist, wenn man von der realen Anschauung ausgeht. Zwar ergibt drei mal sieben gleich viel wie sieben mal drei, aber mit den Stäbchen veranschaulicht, lege ich im ersten Fall drei schwarze, im zweiten aber sieben hellgrüne. Routinierte Mathematiker sehen bloss zwei Faktoren und ein Produkt, aber der Rechenanfänger muss real und auch in der Vorstellung handeln können, und das kann er nur, wenn das Zeichen der Multiplikation „mal“ einen Inhalt hat. Daher muss man, wenn die Schüler später bei angewandten Aufgaben nicht immer wieder Probleme haben sollen, die Bedeutung des Wörtchens „mal“ zuerst (und immer wieder) in andern als arithmetischen Zusammenhängen üben, z.B. indem man die Schüler auffordert, sich drei mal am Ohr zu zupfen, fünf mal einen Ton auf dem Klavier anzuschlagen, das Fenster vier mal zu öffnen usf. Als Übergang zum Rechnen fungiert dann die Aufforderung, z.B. sechs mal ein Zehnerstäbchen aus der Schachtel zu nehmen.

Ich habe in den letzten Jahren oft mit Viert- oder Fünftklässlern, die Mühe in Mathematik hatten, gerechnet und bin dabei immer wieder auf das Phänomen gestossen, dass sie überhaupt keinen Begriff davon haben, was dieses täglich gebrauchte „Mal“ eigentlich bedeutet. So kann es durchaus vorkommen, dass der verwirrte Schüler in der eingekleideten Aufgabe zwei Zahlen sieht und dann beinahe zufällig rätselt, ob er sie nun multiplizieren oder dividieren soll. Ist man aber von Anfang an genau im Anschauen und dem darauf basierenden Denken, dann abstrahiert z.B. der Drittklässler bei der Frage nach der Länge eines Gartenweges, bestehend aus 12 60 cm langen Platten, richtig, indem er schreibt 12 x 60 cm. Zwar würde auch 60 x 12 cm zum richtigen Resultat führen, aber diese Multiplikation bildet nicht das ab, was durch Anschauung und Sprache vorgegeben ist. Wer keinen Sinn für solche Differenzen hat, wird es schwer haben, sich in die Schwierigkeiten eines Anfängers oder gar eines lernschwachen Kindes hineinzudenken und ihm dabei wirksam zu helfen. Auf dieser Stufe bedeutet in einer einfachen Multiplikation der erste Faktor grundsätzlich die Anzahl, der zweite die Einheit. Hinsichtlich der realen Bedeutung von „mal“ ist eine Rechnung wie 7cm mal fünf, genau genommen, ohne Sinn, d.h. gleich sinnlos wie etwa die Aufforderung: Stampfe 7 cm mal auf den Boden.

Analog zur Unterscheidung zweier Faktoren hinsichtlich Anzahl und Einheit ist bei der Division zu unterscheiden zwischen Messen und Teilen. Mir ist bewusst, dass der Mathematiker, der rein abstrakt operiert und sich auch bei der Vertauschung von Faktoren gemäss dem Kommutativgesetz unter dem Operationszeichen „mal“ nichts Konkretes mehr vorstellt oder denkt, die Unterscheidung nicht (mehr) macht. Aber ein Mathematikunterricht, der elementar sein will und darum auf der Anschauung aufbaut, muss hier genau sein. Es ist durchaus etwas anderes, ob ich eine bestimmte Menge (Anzahl) in z.B. drei Teile teile oder ob ich mich vergewissere, wie oft die Einheit drei in dieser Menge enthalten ist. Im allgemeinen macht der elementare Rechenunterricht diesen Unterschied im Zusammenhang mit Masseinheiten bewusst (3 m geteilt durch 5 = 60 cm / 3 m gemessen mit 60 cm = 5 mal), aber der Umgang mit den Farbenstäbchen zeigt, dass man gar nicht auf Masse angewiesen ist, um den Unterschied zu zeigen. Lege ich z.B. ein Zahlfeld von 3 blauen Stäbchen (3 x 9), so sind real als Division nur möglich:

aber nicht:

Will ich die letzten beiden Rechnungen veranschaulichen, muss ich von einem hellgrünen Zahlfeld (9 x 3) ausgehen. Mathematisch heisst dies: Mache ich eine Multiplikation durch eine Division rückgängig, so teile ich, wenn ich den ersten Faktor (die Anzahl) zum Divisor wähle, und ich messe, wenn ich den zweiten Faktor (die Einheit) zum Divisor wähle. Zur Teilungs-Aufgabe „28 geteilt durch 4 gleich 7“ passt als zugehörige Mess-Aufgabe nicht „28 gemessen mit 4 gleich 7 mal“, sondern „28 gemessen mit 7 gleich 4 mal“. Ich habe erfahren, dass es sich in den oberen Klassen auszahlt, hier genau zu sein und sich immer an die Anschauung zu halten.

Das Teilen symbolisieret man mit den Stäbchen am besten, indem man ein Zahlfeld sanft auf den Tisch fallen lässt, so dass der Schüler mit eigenen Augen sieht, wie z.B. bei einem Zahlfeld mit 4 schwarzen Stäbchen vier Teile entstehen.

Beim Messen löst man am besten das Zahlfeld zuerst in eine Linie auf und misst dann mit einem gleichfarbigen Stäbchen, wie oft es Platz hat. Die Sache ist für die Kinder fast zu leicht.

12. Einführung ins Bruchrechnen

Indem wir schon in der 1. Klasse ganz selbstverständlich die Begriffe „die Hälfte von“, „ein Drittel von“, „ein Viertel von“ verwenden, haben wir den Einstieg ins Bruchrechnen eigentlich schon geschafft. Spätestens in der 2. Klasse können wir die Schreibweise der Stammbrüche einführen:

½ von 32 = 16 ¼ von 32 = 8

Sitzen die Stammbrüche, so lassen sich weitere Rechnungen machen:

3/4 von 32 = 24 oder (3/4 von 36) – (¼ von 20) + (½ von 18) = 31

Wir verstehen somit die Brüche zuerst nicht als absolute Zahlen (Bruchteile von 1), sondern als Verhältniszahlen. Auf diese Weise werden die Schüler sehr leicht mit der Welt der Brüche vertraut.

13. Schluss

Zum Schluss weise ich nochmals darauf hin, dass ich hier durchaus nicht den ganzen Mathematikunterricht beschreiben wollte, sondern lediglich die Grundlegung der Arithmetik. Auch das ganze Gebiet der Anwendungen (Sätzchenrechnungen) ist praktisch unberücksichtigt geblieben. In diesem Zusammenhang möchte ich noch anmerken, dass viele Lehrkräfte der Unterstufe bei der Übung arithmetischer Fertigkeiten stets von eingekleideten Aufgaben ausgehen, weil sie glauben, das reine Rechnen mit Zahlen ohne konkrete Beziehung zu realen Dingen sei für Kinder zu wenig motivierend. Ihrer Ansicht nach bequemen sich die Kinder erst dazu, 48 durch 6 zu teilen, wenn sie sich vorstellen dürfen, dass 48 Farbstifte unter 6 Kinder verteilt werden. Ich könnte dieser Argumentation beipflichten, wenn ich nicht erfahren hätte, dass eben das Cuisenaire-Material eine sehr kind- und sachgemässe Veranschaulichung arithmetischer Gegebenheiten ermöglicht. Es hat sich in meiner Praxis gezeigt, dass sich Unterstufenkinder verhältnismässig leicht motivieren lassen, sich mit der Welt der Zahlen auseinanderzusetzen, ohne dass man diese immer mit Äpfeln, Blumen und Schokoladetäfelchen versüssen muss. Ich glaube auch, dass heute viele Kinder auf der Unterstufe klar unterfordert sind und sich eigentlich im Rechenunterricht langweilen. Selbstverständlich ist es unsere Pflicht, durch alle nur erdenklichen Hilfen die schwächeren Schüler zu fördern. Ich meine aber, dass dies nicht auf Kosten jener gehen darf, die gerne stärker gefordert würden. Um diesen Zwiespalt zu lösen, müssen wir – im Rechnen genauso wie in andern Fächern – individualisieren. Die Methode Cuisenaire ist vorzüglich geeignet, sowohl die schwachen als auch die leistungsfähigeren Schüler zu fördern.

Bezugsquelle Schweiz:

Kasten mit 240 Stäben zum Preis von Fr. 39.95 bei:

SCHUBI, Breitwiesenstr. 9, CH – 8007 Schaffhausen

+41 (0)52 644 10 10

service@schubi.ch

Bezugsquelle Deutschland:

Ernst Klett Verlag GmbH, Rotebühlstraße 77, 70178 Stuttgart

Käuflich sind auch kleine Sätze mit farbigen Stäben. Siehe http://www.betzold.de/kleiner-satz-mit-farbigen-staeben/p_85823_122_12200001/betzold-de .

Einmaleins-Kärtchen

Um das Einmaleins zu automatisieren, habe ich Übungskärtchen konzipiert, die man bei mir erwerben kann

Die Kärtchen (6 mal 6 cm) sind auf der einen Seite mit einem Zahlfeld entsprechend den Cuisenaire-Stäben farbig bedruckt, und auf der andern Seite steht die entsprechende Rechnung.

Das vollständige Einmaleins würde 100 Karten umfassen. Um das Üben praktikabler und effizienter zu machen, habe ich den Kartensatz reduziert, indem ich alle Multiplikationen mit den Zahlen 1, 2 und 10 und zusätzlich noch die Multiplikation 3 mal 3 weggelassen habe. Damit umfasst ein Kartensatz 48 Karten.

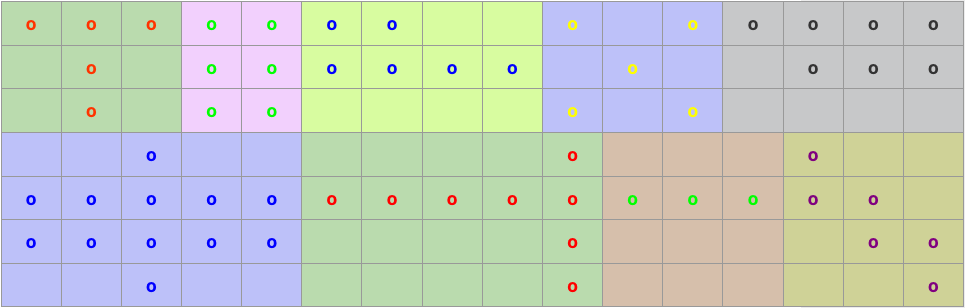
Dem Schüler ist bewusst zu machen, dass das linksseitige, senkrecht zu den Stäben des Zahlfelds stehende Stäbchen nicht zum Produkt gehört, sondern lediglich als Mass dient, um die Anzahl liegender Stäbe im Zahlfeld rasch erfassen zu können. Es empfiehlt sich, so lange mit der Farbdarstellung zu üben, bis die Schüler dies fehlerfrei können, und erst dann – über ein Stadium der zufälligen Durchmischung (siehe Bild oben) – mit den blossen Zahlen zu arbeiten. Sobald das ganze Einmaleins erarbeitet ist, sollen die Schüler möglichst täglich etwa 5 Minuten zum Üben mit den Kärtchen aufwenden, möglichst in Kleingruppen (und gemeinsam mit der Lehrperson) dies über mehrere Monate.

Die Kartenserien (nur noch wenige vorhanden) können bei mir gegen Erlegung der Versandkosten bezogen werden. Bestellen per E-Mail (siehe Kontakt).